1と7のリビジョン間の差分 (その間の編集: 6回)

言語モデル論めも

後半戦を適当にググった内容と考えたことのメモ。
全く授業を聞いてないので間違っていると思う。。

あわせて読みたい

N-gram

http://ja.wikipedia.org/wiki/全文検索#N-Gram
検索のインデックスを作る方法の１つ。
たぶん、vector<string> ss; for(int i = 0; i < (int)ss.size()-k; i++)でss.sub(i,k)をキーにしてインデックスを作る。
形態素解析をするのに比べ、精度も悪いし検索時速度も遅いしインデックスの量も多くなるが、言語に依存しないため実装は楽

N-gramモデル

http://www.shuiren.org/chuden/teach/n-gram/index-j.html
「ある文字列の中で、N個の文字列または単語の組み合わせが、どの程度出現するか」を調査する言語モデル
「近くにある確率の高い単語の組み合わせはある」という仮定に基づいている。

Zipfの法則

http://ja.wikipedia.org/wiki/ジップの法則
k番目に多い要素が全体に占める割合は1/kに比例するという経験則らしい。

ロングテール

http://ja.wikipedia.org/wiki/ロングテール
全体に占める割合が少ない要素はたくさんあることを示している言葉だと思う。

スムージング

http://www.r.dl.itc.u-tokyo.ac.jp/~nakagawa/SML/smoothing.pdf(pdf注意)
標本データはでこぼこしているので、ならす。その操作。
また、標本値は０でも、実際の値は０でないものはたくさんあるので、ありそうなものを表に加え、すべての標本値にεを加える操作が特に重要。これを実現する方法の１つに、バックオフスムージングがある。

バックオフスムージング

N-gramモデルにおいて標本値が０であるものの標本値を、(N-1)-gramモデルから推定する手法。

統計的機械学習

http://www.r.dl.itc.u-tokyo.ac.jp/node/33
http://www.r.dl.itc.u-tokyo.ac.jp/~nakagawa/SML/index-SML.html
http://ja.wikipedia.org/wiki/機械学習
機械学習にはだいたい３種類ある

教師あり学習
教師なし学習
強化学習（半教師あり学習とも？）

特徴ベクトル

なんらかの標本の値を、１次元の値ではなく、多次元のベクトルにすると捗る。
例えば、以降に出てくるパターン認識の話では、各標本をn次元空間の点にマップして(ｎ次元ベクトルにして)、標本をAとBという集合に分ける操作を、決定境界（ｎ次元空間上の面）を決める操作に還元している。

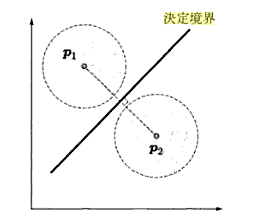
特徴空間, 決定境界

特徴空間は、標本値をｎ次元ベクトルにした時のｎ次元空間。決定境界は、とりあえず、この図で分かった気になる

線形分類器

http://ja.wikipedia.org/wiki/線形分類器
線形識別器とも。
決定境界を線形（平面）と仮定した時に、その境界を求めるアルゴリズム。

パーセプトロン

http://ja.wikipedia.org/wiki/パーセプトロン
http://d.hatena.ne.jp/AntiBayesian/20111125/1322202138
一般的な説明？としては、「ニューラルネットの一種。脳と視覚の機能をモデル化したものであり、パターン認識を行う」らしい。
線形分類器の１つ。適当に決めた境界を少しずつ改善していって境界を決めるアルゴリズム。
詳しくは、２つめのリンク参照。

ログ線形モデル

http://d.hatena.ne.jp/jetbead/20110923/1316794767
http://www.psy.ritsumei.ac.jp/~hoshino/spss/log_00.html
対数線形モデルとも（？）
Y = a * b ^ Xというようなモデル。

サポートベクトルマシン

http://ja.wikipedia.org/wiki/サポートベクターマシン
http://www.neuro.sfc.keio.ac.jp/~masato/study/SVM/index.htm
略してSVM。教師あり学習を用いる識別手法の一つ。（パーセプトロンと結果は似てる。）
詳しくは、２つめのリンクを参照。
他の識別手法と比べてユニークな点として、「マージン最大化」があげられる。

隠れマルコフモデル

http://ja.wikipedia.org/wiki/隠れマルコフモデル
これはさすがに知ってる。

ビタビアルゴリズム

http://ja.wikipedia.org/wiki/ビタビアルゴリズム
隠れマルコフモデルのパラメータが既知で、観測された事象の列が与えられた時、状態（通常賽？シゴロ賽？）の遷移のうちもっとも尤もらしいものを推定するアルゴリズム。DP。

教師あり学習, 教師なし学習

http://ja.wikipedia.org/wiki/教師あり学習
http://ja.wikipedia.org/wiki/教師なし学習
なんとなく意味は分かる。

EMアルゴリズム

http://ja.wikipedia.org/wiki/EMアルゴリズム
よくわからない

前向き確率, 後ろ向き確率

http://anlp.jp/NLP_Portal/glossary/index.html

隠れマルコフモデル(HMM, hidden markov model)において，初期ノードからあるノードまでにある時系列データが生成される確率のことを前向き確率という．トレリス上を前向きに辿り動的計画法により順次求めることから前向きという名前が付いている．同様に，後向きに辿る後向き確率(backward probability)もある．隠れマルコフモデルのパラメータ推定アルゴリズム(Baum-Welchアルゴリズム)では，前向き/後向き確率両方を用いてパラメータ推定に必要な確率を計算する．

自然言語処理

http://ja.wikipedia.org/wiki/自然言語処理

構文解析

http://ja.wikipedia.org/wiki/構文解析

文脈自由文法

http://ja.wikipedia.org/wiki/文脈自由文法
＼文脈自由文法／

CKY法

http://ja.wikipedia.org/wiki/CYK法
L*LF*S...

確率文脈自由文法

http://ja.wikipedia.org/wiki/確率文脈自由文法
各生成規則に確率があって、より尤もらしい構文解析が可能。になりそう

ビタビアルゴリズム

再び。CKYはboolのdpだけど、それを確率でやるとかだろうか

情報検索

http://ja.wikipedia.org/wiki/情報検索

転置インデックス

http://ja.wikipedia.org/wiki/転置インデックス
wikipediaの例がわかりやすい。何が転置なのかよくわからない

接尾辞配列

http://ja.wikipedia.org/wiki/接尾辞配列
suffix arrayとも。接尾辞の検索がO(n)で出来るようになる。前処理は普通にやるとO(nlogn)だけど、O(n)で出来るとか授業で言ってた。

ベクトル空間モデル

http://ja.wikipedia.org/wiki/ベクトル空間モデル
http://c-faculty.chuo-u.ac.jp/~saitotac/2003Gradu/matsuda/4no5.htm
読めば分かりそう。

リンク解析

<a href="http://is2011.2-d.jp"> 情報科学科2011関係の便利情報満載のwiki! </a>

ってなってたら、まあ分かりますよねという話（？）

ランク学習

http://www.slideshare.net/sleepy_yoshi/dsirnlp1
http://www.slideshare.net/tkng/confidence-weighted
PageRank的な話？あとで読む。

クラスタリング

http://ja.wikipedia.org/wiki/データ・クラスタリング
http://ja.wikipedia.org/wiki/ウォード法
http://ja.wikipedia.org/wiki/K平均法
クラスタリングの意味はなんとなく分かる。

Categoryノート

fujima/知能システム論 (最終更新日時 2012-01-25 11:31:15 更新者 fujima)

-  ⇤ ← 2012-01-25 08:02:52時点のリビジョン1 → 
  サイズ: 7274
  編集者: fujima
  コメント:
+   ← 2012-01-25 11:14:48時点のリビジョン7 → ⇥
  サイズ: 8529
  編集者: fujima
  コメント:
-削除された箇所はこのように表示されます。
+追加された箇所はこのように表示されます。
 行 11:
-== とりあえず ==
+=== あわせて読みたい ===
 行 19:
+== N-gramモデル ==
[[http://www.shuiren.org/chuden/teach/n-gram/index-j.html]]<<BR>>
「ある文字列の中で、N個の文字列または単語の組み合わせが、どの程度出現するか」を調査する言語モデル<<BR>>
「近くにある確率の高い単語の組み合わせはある」という仮定に基づいている。<<BR>>
-行 29:
+行 34:
-謎。統計データの凹凸をならすと式を推定しやすくなりそうなので、そのならす段階のこと？<<BR>>
+[[http://www.r.dl.itc.u-tokyo.ac.jp/~nakagawa/SML/smoothing.pdf]](pdf注意)<<BR>>
標本データはでこぼこしているので、ならす。その操作。<<BR>>
また、標本値は０でも、実際の値は０でないものはたくさんあるので、ありそうなものを表に加え、すべての標本値にεを加える操作が特に重要。これを実現する方法の１つに、バックオフスムージングがある。<<BR>>
-行 31:
+行 38:
-== ん？ ==
なんかおかしい。
「言語モデル　スムージング」でググったら色々でてきた<<BR>>
[[http://unicorn.ike.tottori-u.ac.jp/2009/s062041/paper/graduation-thesis/node11.html]]<<BR>>
[[http://unicorn.ike.tottori-u.ac.jp/2009/s062041/paper/graduation-thesis/node17.html]]<<BR>>
[[http://unicorn.ike.tottori-u.ac.jp/2009/s062041/paper/graduation-thesis/node24.html]]<<BR>>
よくわからない。。とりあえず飛ばす。<<BR>>
+=== バックオフスムージング ===
N-gramモデルにおいて標本値が０であるものの標本値を、(N-1)-gramモデルから推定する手法。<<BR>>
-行 46:
+行 48:
- *強化学習（またの名を半教師あり学習？）
+ *強化学習（半教師あり学習とも？）
-行 49:
+行 51:
-って何だろう。。<<BR>>
[[http://www.nal.ie.u-ryukyu.ac.jp/wiki/index.php?yono%2FPython%A4%C7%BC%AB%C1%B3%B8%C0%B8%EC%BD%E8%CD%FD | http://www.nal.ie.u-ryukyu.ac.jp/wiki/index.php?yono/Pythonで自然言語処理]]<<BR>>
この人は、
{{{
文書における特徴ベクトルは，多くの場合文書中の単語を要素，重みとして出現頻度やTF-IDFによって表現されます．
}}}
と書いているが。。<<BR>>
+なんらかの標本の値を、１次元の値ではなく、多次元のベクトルにすると捗る。<<BR>>
例えば、以降に出てくるパターン認識の話では、各標本をn次元空間の点にマップして(ｎ次元ベクトルにして)、標本をAとBという集合に分ける操作を、決定境界（ｎ次元空間上の面）を決める操作に還元している。<<BR>>

== 特徴空間, 決定境界 ==
特徴空間は、標本値をｎ次元ベクトルにした時のｎ次元空間。
決定境界は、とりあえず、この図で分かった気になる<<BR>>
{{attachment:ketteikyoukai.png}}
-行 59:
+行 61:
-よくわからない
+線形識別器とも。<<BR>>
決定境界を線形（平面）と仮定した時に、その境界を求めるアルゴリズム。
-行 63:
+行 66:
-「ニューラルネットの一種。脳と視覚の機能をモデル化したものであり、パターン認識を行う」らしい。<<BR>>

== 特徴空間, 決定境界 ==
なにやら、パターン認識の話らしい。<<BR>>
とりあえず、この図で分かった気になる<<BR>>
+[[http://d.hatena.ne.jp/AntiBayesian/20111125/1322202138]]<<BR>>
一般的な説明？としては、「ニューラルネットの一種。脳と視覚の機能をモデル化したものであり、パターン認識を行う」らしい。<<BR>>
線形分類器の１つ。適当に決めた境界を少しずつ改善していって境界を決めるアルゴリズム。<<BR>>
詳しくは、２つめのリンク参照。
-行 70:
+行 72:
-対数線形モデルとも（？）
 Y = a * b ^ Xみたいなモデルっぽい。
+[[http://d.hatena.ne.jp/jetbead/20110923/1316794767]]<<BR>>
[[http://www.psy.ritsumei.ac.jp/~hoshino/spss/log_00.html]]<<BR>>
対数線形モデルとも（？）<<BR>>
Y = a * b ^ Xというようなモデル。<<BR>>
-行 75:
+行 79:
-略してSVM。教師あり学習を用いる識別手法の一つ。めっちゃ強い。<<BR>>
+[[http://www.neuro.sfc.keio.ac.jp/~masato/study/SVM/index.htm]]<<BR>>
略してSVM。教師あり学習を用いる識別手法の一つ。（パーセプトロンと結果は似てる。）<<BR>>
詳しくは、２つめのリンクを参照。<<BR>>
他の識別手法と比べてユニークな点として、「マージン最大化」があげられる。<<BR>>
-行 83:
+行 90:
-隠れマルコフモデルのパラメータが既知で、観測された事象の列が与えられた時、状態（通常骰？シゴロ骰？）の遷移のうちもっとも尤もらしいものを推定するアルゴリズム。DP。<<BR>>
+隠れマルコフモデルのパラメータが既知で、観測された事象の列が与えられた時、状態（通常賽？シゴロ賽？）の遷移のうちもっとも尤もらしいものを推定するアルゴリズム。DP。<<BR>>
-行 140:
+行 147:
-たぶん、ページを頂点リンクを辺としたグラフを考えるんだろう<<BR>>
ぐぐってもノイズしかヒットしなくてうざい
+{{{
<a href="http://is2011.2-d.jp"> 情報科学科2011関係の便利情報満載のwiki! </a>
}}}
ってなってたら、まあ分かりますよねという話（？）

"fujima/知能システム論"の差分

言語モデル論めも

あわせて読みたい

N-gram

N-gramモデル

Zipfの法則

ロングテール

スムージング

バックオフスムージング

統計的機械学習

特徴ベクトル

特徴空間, 決定境界

線形分類器

パーセプトロン

ログ線形モデル

サポートベクトルマシン

隠れマルコフモデル

ビタビアルゴリズム

教師あり学習, 教師なし学習

EMアルゴリズム

前向き確率, 後ろ向き確率

自然言語処理

構文解析

文脈自由文法

CKY法

確率文脈自由文法

ビタビアルゴリズム

情報検索

転置インデックス

接尾辞配列

ベクトル空間モデル

リンク解析

ランク学習

クラスタリング